Horizontal line test

In mathematics, the horizontal line test is a test used to determine if a function is injective^[1] and/or surjective. The lines used for the test are parallel to the x axis.

Consider a function f : X → Y with its corresponding graph as a subset of the Cartesian product X x Y. Consider the horizontal lines in X x Y : .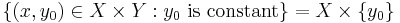

• The function f is injective (i.e., one-to-one) if and only if it can be visualized as one whose graph intersects any horizontal line at MOST once.
• The function f is surjective (i.e., onto) if and only if its graph intersects any horizontal line at LEAST once.
• f is bijective if and only if any horizontal line will intersect the graph EXACTLY once.

This test is also used to determine whether or not the inverse relation of a function is itself a function.

See also

• Vertical line test
• Function (mathematics)
• Inverse (mathematics)

References